The next equality constraint we will derive is the pulley constraint. A pulley constraint can be used to join two bodies at a fixed distance. In addition, the constraint can be used to simulate a block-and-tackle.
- Problem Definition
- Process Overview
- Position Constraint
- The Derivative
- Isolate The Velocities
- Compute The K Matrix
Problem Definition
It’s probably good to start with a good definition of what we are trying to accomplish.
We want to take two or more bodies and constrain their motion in some way. For instance, say we want two bodies to only be able to rotate about a common point (Revolute Joint). The most common application are constraints between pairs of bodies. Because we have constrained the motion of the bodies, we must find the correct velocities, so that constraints are satisfied otherwise the integrator would allow the bodies to move forward along their current paths. To do this we need to create equations that allow us to solve for the velocities.
What follows is the derivation of the equations needed to solve for a Pulleyconstraint.
Process Overview
Let’s review the process:
- Create a position constraint equation.
- Perform the derivative with respect to time to obtain the velocity constraint.
- Isolate the velocity.
Using these steps we can ensure that we get the correct velocity constraint. After isolating the velocity we inspect the equation to find J, the Jacobian.
Most constraint solvers today solve on the velocity level. Earlier work solved on the acceleration level.

Once the Jacobian is found we use that to compute the K matrix. The K matrix is the A in the Ax = b general form equation.
Position Constraint
So the first step is to write out an equation that describes the constraint. A Distance Joint should allow the two bodies to move and rotate freely, but should keep them at a certain distance from one another. For a Pulley Joint its similar except that the bodes distance is constrained to two axes. In the middle we will allow the option of a block-and-tackle. Examining the image to the right, we see that there are two bodies: Ba, Bb who have distance constraints that are along axes: Ua, Ub which were formed from the Ground and Body anchor points: GAa, GAb, BAa, BAb.
Given this definition we can see that the direction of Ua and Ub can change if the bodies swing left or right for example.
Unlike the Distance Joint, a Pulley Joint allows the distances from the ground anchors to the body anchors to increase and decrease (the magnitude of Ua and Ub can also change). However, the total distance along the two axes must be equal to the initial distance when the joint was created (this is what we are trying to constrain). If we apply some scalar factor (or ratio) to the distances we can simulate a block-and-tackle.
We can represent this constraint by the following equation:

Where:



Where  are the length of Ua, body a’s body anchor point, body a’s ground anchor point, and the vector Ua respectively.
are the length of Ua, body a’s body anchor point, body a’s ground anchor point, and the vector Ua respectively.
Likewise  are the length of Ub, body b’s body anchor point, body b’s ground anchor point, and the vector Ub respectively.
are the length of Ub, body b’s body anchor point, body b’s ground anchor point, and the vector Ub respectively.
 is computed once when the joint is created to obtain the target total length of the pulley.
is computed once when the joint is created to obtain the target total length of the pulley.
Finally  is a scalar ratio value that will allow us to simulate a block-and-tackle.
is a scalar ratio value that will allow us to simulate a block-and-tackle.
To review, our position constraint calculates the current lengths of the two axes (applying the ratio to one) and subtracts it from the initial to find how much the constraint is violated.
The Derivative
The next step after defining the position constraint is to perform the derivative with respect to time. This will yield us the velocity constraint.
The velocity constraint can be found/identified directly, however its encouraged that a position constraint be created first and a derivative be performed to ensure that the velocity constraint is correct.
Another reason to write out the position constraint is because it can be useful during whats called the position correction step; the step to correct position errors (drift).
Taking the derivative of our position constraint we get:

Then just to clean up a bit:

Now we need to perform the derivative on  . If we remember
. If we remember  was defined as:
was defined as:


So let’s side step for a minute and perform the derivative of  :
:

We needed to use the chain rule in order to fully compute the derivative where the derivative of u:

The derivative of a fixed length vector under a rotation frame is the cross product of the angular velocity with that fixed length vector.
Note here that the g vector (ground anchor) is constant and therefore becomes the zero vector.
In the last few steps I replaced a portion of the equation with:

In addition, I replaced the dot product with a matrix multiplication by:

Now if we substitute back into the original equation we get:

Isolate The Velocities
The next step involves isolating the velocities and identifying the Jacobian. This may be confusing at first because there are two velocity variables. In fact, there are actually four, the linear and angular velocities of both bodies. To isolate the velocities we will need to employ some identities and matrix math.
The linear velocities are already isolated so we can ignore those for now. The angular velocities on the other hand have a pesky cross product. In 3D, we can use the identity that a cross product of two vectors is the same as the multiplication by a skew symmetric matrix and the other vector; see . For 2D, we can do something similar by examining the cross product itself:
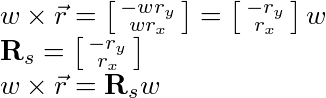
Remember that the angular velocity in 2D is a scalar.
Removing the cross products using the process above yields:

Now, just to clean up some, if we inspect:

Now replacing what we found above into the original equation (and some clean up):

Now if we employ some matrix multiplication we can separate the velocities from the known coefficients:

Now, by inspection, we obtain the Jacobian:

Compute The K Matrix
Lastly, to solve the constraint we need to compute the values for A (I use the name K) and b:
See the “Equality Constraints” post for the derivation of the A matrix and b vector.
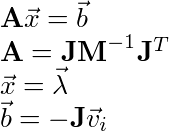
The b vector is fairly straight forward to compute. Therefore I’ll skip that and compute the K matrix symbolically:

Multiplying left to right the first two matrices we obtain:

Multiplying left to right again:

If we simplify using:

Remember the inertia tensor in 2D is a scalar, therefore we can pull it out to the front of the multiplications.

Plug the values of the K matrix and b vector into your linear equation solver and you will get the impulse required to satisfy the constraint.
Note here that if you are using an iterative solver that the K matrix does not change over iterations and as such can be computed once each time step.
Another interesting thing to note is that the K matrix will always be a square matrix with a size equal to the number of degrees of freedom (DOF) removed. This is a good way to check that the derivation was performed correctly.
Hi, I am trying to implement Pulley joint in a physics simulator. This post has been very helpful.
Could you derive the expression for (del_J / del_t) i.e. the time derivative of the jacobian matrix.
My implementation is giving very erratic behaviour which I suspect is because of the incorrect value of
time-derivative of the jacobian-matrix.
I’m not sure I understand what you are asking. Why do you need the time derivative of the Jacobian? For this particular instance we only need the time derivative of the constraint, then we identify the Jacobian and then plug it into our equality constraints formulation. Can you elaborate a bit more one what you are looking for?
William
Actually, I am working on STEP (a physics simulator). Its constraintsolver calculates the ‘b’ vector as :
b = info->jacobian * info->acceleration;
b += info->jacobianDerivative * info->velocity;
b = – (b + info->value + info->derivative);
(‘info’ is a pointer to a structure here)
Hmm, I’m not familiar with STEP, but perhaps I can give some pointers. It looks like these three steps are computing the right side of the Equality Constraint:
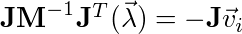
I could be wrong, but I think the info->jacobianDerivative is referring to what I have derived in this post.

From the source there its hard to tell what that first and last operations are. I’m guessing they are including external forces or some sort of bias factors or another ODE for stability.
You can see my full implementation if you would like a reference. The meat is in the
initializeConstraintsand thesolveVelocityConstraintsmethods.Hope that helps,
William
Oops, I was making a silly mistake somewhere else in the code. It is working fine now :) .
jacobianderivative in the case of my solver is the time-derivative of the jacobian matrix . Deriving it is simple ( after I gave it some clear thinking ) , simply take each term of the jacobian-matrix and find its time-derivative.
Thanks for such descriptive post William, It helped me a lot in understanding how the constraint deriving works, (specially the part where you find the ‘jacobian’ from ‘C_dot’ by separating the velocities) :)
I am also trying add friction-force to STEP . Could you help me out in deriving the values of ‘C’ , ‘C_dot’, and ‘J’ for that?
I took a look at this implementation
but I don’t understand how it has been derived. I understand how ‘C_dot’ has been derived ( quite obvious ) but the jacobian — J = [-I -r1_skew I r2_skew ] is too misty for me. ( pardon me if it is obvious but I am unexperienced about these stuff ). Could you help me with the derivation of the jacobian-matrix for this case ?
Also, why are they taking a different equation for the angle-constraint –
”
// Angle constraint
// Cdot = w2 – w1
// J = [0 0 -1 0 0 1]
// K = invI1 + invI2
”
why not accomodate it in the previous constraint itself?
Also, I don’t see any place where they have made use of the friction-coefficient between the bodies.
Part of the confusion here is what the FrictionJoint is designed to do:
The FrictionJoint in farseer, box2d, dyn4j, etc. is a constraint that drives the linear and angular velocities to zero. Instead of supplying a friction coefficient, you supply a maximum torque and force that the joint can apply to reduce the velocities.
Given that, its really just a combination of the Point-to-Point constraint and the Angle constraint:
[ 1 r_skew -1 -r_skew ]
[ 0 1 0 -1 }
This will compute the impulse required to fix the bodies in place (the Weld constraint). But if we clamp the linear and angular impulse by the maximum force/torque it will give the effect of friction.
In general, the friction constraint constrains all 3 degrees of freedom (for 2D), translation along the x and y and rotation about z. In this case we can solve them separately to make things easier. You can also reference the implementation in dyn4j . Focus your attention on the solveVelocityConstraints method.
William